Introduction

The atmosphere is in motion and it is a continuous mixing and clashing of vortices and structures, but when it is averaged over a long period of time (see Figure below) it shows a remarkable simple structure.

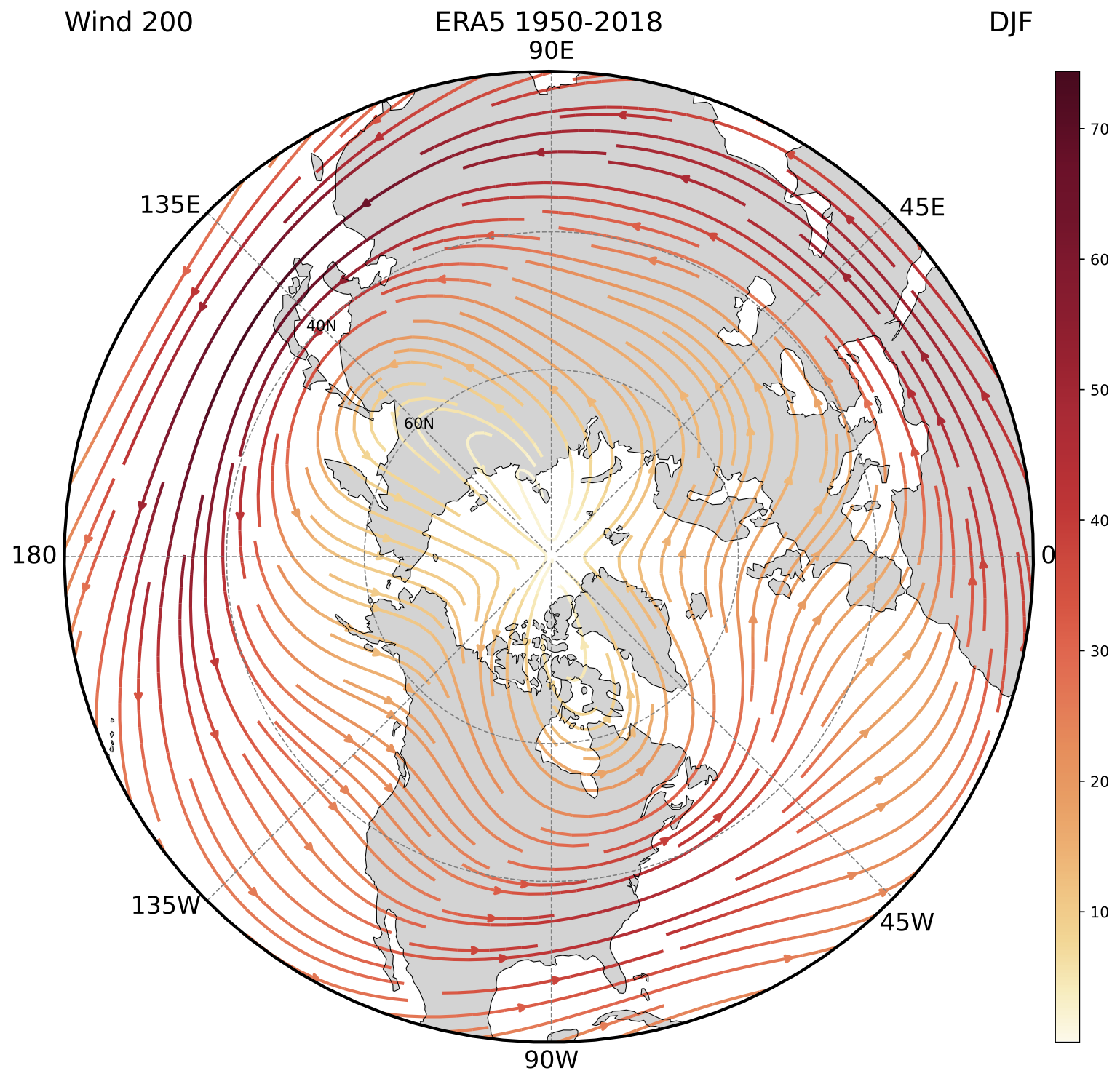
The figure shows the wind at an approximate level of about $12$ km, that is considered to be in the free atmosphere, far from the influence of the ground. The circulation is a large vortex around the pole that shows small oscillation in latitudes, especially pronounced over North America and the Asian Pacific Coast. The flow is therefore predominantly in the East-West direction, with a relatively small component in the meridional direction. The circumpolar vortex has been one of the first structures to be recognized when plentiful observations of the upper air flow became available, but it provided some of the intriguing questions that drove the development of geophysical fluid dynamics to this time. some of them have not been completely understood.

• What is maintaining this peculiar circulation ?
• Which factor determines the amplitude and location of the undulations in meridional direction ? Some of these question will be addressed in these notes.

Coordinate systems

Spherical Coordinates

The most commonly used coordinate system for the analysis of the atmosphere and the oceans is a spherical coordinate system attached to the rotating Earth (see Figure below).

The spherical coordinates are slightly different from the usual mathematical ones as the latitude is measured from the equator and therefore it can take negative values. The longitude is running west to east.

The longitude is also known as the “zonal” direction whereas the latitude is also known as the “meridional” direction. Winds are identified by the direction they are coming from, so a “westerly” wind is coming from the West and an “easterly” wind is coming from the East.

This coordinate system is rotating with the Earth and therefore it generates force terms in any dynamical equation expressed in this system of coordinate, the Coriolis terms.

The $\beta$-plane

It is sometimes convenient to shift coordinate system if the latitudinal extension of the motion is not too great with respect to the motion parameters as they are expressed in the adimensional numbers. When this is possible, a tangent coordinate system is applied at a specific latitude ${\varphi }_0$ and the resultant Cartesian coordinates system is called the $\beta$-plane. Usually symbols $(x,y)$ are used in this case for the zonal and meridional coordinate. In the $\beta$-plane the planetary vorticity $f$ is linearized as $f=f_0+\beta y$, where $\beta =\frac{\partial f}{\partial y}({\varphi }_0)$.

Advective derivative

To describe the governing equation of the atmosphere and eventually of the ocean we have to understand how we write the rate of change with time of this fluid. This problem was solved by considering the fact that the rate of change in the fluid cannot be seen as arate of change with respect to a fixed system of coordinate because the system is moving with the fluid itself. Therefore, first we have to find a way to describe the change taking into account the moving system of restaurants. These can be done by using a concept developed in the 19th century by Euler that is called “advective derivative” that can be obtained from a total derivative of the property,

$$\frac{d\varphi }{dt}=\frac{\partial \varphi }{\partial t}+\frac{\partial x}{\partial t}\frac{\partial \varphi }{\partial x}+\frac{\partial y}{\partial t}\frac{\partial \varphi }{\partial y}+\frac{\partial z}{\partial t}\frac{\partial \varphi }{\partial z}=\frac{\partial \varphi }{\partial t}+\mathbf{v}\cdot \nabla \varphi$$

and so it can be defined as

$$\frac{D\phi }{Dt}=\frac{\partial \phi }{\partial t}+\mathbf{v}\cdot \nabla \phi$$

in this way the moving fluid can be described by derivatives with respect the “fixed” coordinate system, i.e. the Eulerian description. The alternative description of the observer moving with fluid is known as the “Lagrangian” description.

Primitive Equations

The equation governing the motion of the atmosphere can be written as:

$$\begin{array}{rl}& \frac{Du}{Dt}-\frac{uv\tan \varphi }{r}+\frac{uw}{r}=-\frac{1}{\rho r\cos \varphi }\frac{\partial p}{\partial \lambda }+fv-\hat{f}w+F_{\lambda }\\ & \frac{Dv}{Dt}-\frac{u^2\tan \varphi }{r}+\frac{vw}{r}=-\frac{1}{\rho r}\frac{\partial p}{\partial \varphi }-fu+F_{\varphi }\\ & \frac{Dw}{Dt}-\frac{u^2+v^2}{r}=-\frac{1}{\rho }\frac{\partial p}{\partial z}-g+\hat{f}u+F_z\end{array}$$

the $f=2\Omega \sin \varphi$ and $\hat{f}=2\Omega \cos \varphi$ terms arise from the rotating spherical coordinate system that we have chosen, other terms are generated by the spherical geometry. Some of them are small and traditionally they can be neglected, so that we arrive at the system

$$\begin{array}{rl}& \frac{Du}{Dt}-v\left(f+\frac{u\tan \varphi }{a}\right)=-\frac{1}{\rho a\cos \varphi }\frac{\partial p}{\partial \lambda }+F_{\lambda }\\ & \frac{Dv}{Dt}+u\left(f+\frac{u\tan \varphi }{a}\right)=-\frac{1}{\rho a}\frac{\partial p}{\partial \varphi }+F_{\varphi }\\ & \frac{Dw}{Dt}=-\frac{1}{\rho }\frac{\partial p}{\partial z}-g+F_z\end{array}$$

where we have also used the Shallowness Approximation by assuming $r=a+z\approx a$, where $a$ is the Earth radius.

However the advective derivative must be expressed in spherical coordinates

$$\frac{D}{Dt}=\frac{\partial }{\partial t}+\frac{u}{a\cos \varphi }\frac{\partial }{\partial \lambda }+\frac{v}{a}\frac{\partial }{\partial \varphi }+w\frac{\partial }{\partial z}$$

so that the velocity components are

$$\begin{array}{rl}& u=a\cos \varphi \frac{\partial \lambda }{\partial t}\\ & v=a\frac{\partial \varphi }{\partial t}\\ & w=\frac{\partial z}{\partial t}\end{array}$$

These equation govern the mechanical behavior of the atmosphere, and we will see in a different form, also of the ocean. There three forces in action: pressure gradient, rotation via the Coriolis force and gravity.

The equation are not complete, we have three equation but five variables, so we need to find the missing relations. We are using the basic conservation principles, the latter equations describe the conservation of momentum, we can exploit the conservation of mass. The mass of the fluid must be conserved locally, because there are now sinks or sources in the atmosphere itself, so we want to write the mass of a volume of atmosphere fixed in space as

$$M={\int }_V\rho dV$$

the mass in the volume can only change if there is a flux of mass at surface $S$,

$$\frac{\partial }{\partial t}{\int }_V\rho dV=-{\int }_S\rho \mathbf{v}\cdot ndS$$

using the divergence theorem however we have

$$\frac{\partial }{\partial t}{\int }_V\rho dV=-{\int }_V\nabla \cdot (\rho \mathbf{v})dV$$

because the volume is not changing with time we can bring the derivative inside the integral and we get

$${\int }_V\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})dV=0$$

but the volume is arbitrary, so it must be that

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0$$

is valid locally.

We have still at our disposal the conservation of thermodynamical energy and so we can also use

$$C_v\frac{DT}{Dt}=-p\frac{D}{Dt}\left(\frac{1}{\rho }\right)+Q$$

where we included the temperature and heating/cooling term $Q$. The state variable are then linked by the state equation

$$p=\rho RT$$

where $R$ is the gas constant for dry air.

We can use the equation of state to write the energy equation ( or the temperature equation) in a different form,

$$c_v\frac{DT}{Dt}=-p\frac{D}{Dt}\left(\frac{RT}{p}\right)+Q=-R\frac{DT}{Dt}+\frac{RT}{p}\frac{Dp}{Dt}+Q$$

yielding the alternative forms ( since $c_p=c_v+R$),

$$c_p\frac{DT}{Dt}-\frac{1}{\rho }\frac{Dp}{Dt}=Q$$

For adiabatic processes $Q=0$ and so

$$\begin{array}{rl}& c_p\frac{DT}{Dt}-\frac{1}{\rho }\frac{Dp}{Dt}=0\\ & \frac{c_p}{T}\frac{DT}{Dt}-\frac{R}{p}\frac{Dp}{Dt}=0\\ & \frac{D}{Dt}\log T-\frac{R}{c_p}\frac{D}{Dt}\log p=0\end{array}$$

integrating it we get

$$\log T/T_0-\log {\left(\frac{p}{p_0}\right)}^{R/c_p}=const$$

or

$$\frac{T}{T_0}{\left(\frac{p_0}{p}\right)}^{R/c_p}=const$$

so the quantity, known as potential temperature

$$\theta =T{\left(\frac{p_0}{p}\right)}^{R/c_p}$$

is conserved in adiabatic processes and the thermodynamics equation can be written as

$$\frac{D\theta }{Dt}=Q$$

Hydrostatic balance

Under the action of gravity the vertical component of the pressure gradient force balances the action of gravity, resulting in very small vertical acceleration

$$\frac{\partial p}{\partial z}=-g\rho$$

then if we take the vertical derivative of the Equation above

$$\frac{1}{T_0}\frac{dT}{dz}{\left(\frac{p_0}{p}\right)}^{R/c_p}-\frac{p_0}{p^2}\frac{R}{c_p}\frac{T}{T_0}{\left(\frac{p_0}{p}\right)}^{R/c_p-1}\frac{dp}{dz}=0$$

simplifying

$$\frac{dT}{dz}-\frac{p_0}{p^2}\frac{R}{c_p}T{\left(\frac{p_0}{p}\right)}^{-1}\frac{dp}{dz}=0$$

or

$$\frac{dT}{dz}-\frac{1}{p}\frac{R}{c_p}T\frac{dp}{dz}=\frac{dT}{dz}+g\rho \frac{1}{p}\frac{R}{c_p}T=0$$

but using the equation of state

$$\frac{dT}{dz}=-\frac{g}{c_p}$$

that gives how the temperature change with height under adiabatic conditions and when the hydrostatic balance is valid. This is known as the adiabatic lapse rate.

Summary of fundamental equations

Summarizing our discussion, the fundamental equation that describe the motion of the atmosphere then are:

$$\begin{array}{rl}& \frac{Du}{Dt}-v\left(f+\frac{u\tan \varphi }{a}\right)=-\frac{1}{a\cos \varphi }\frac{1}{\rho }\frac{\partial p}{\partial \lambda }+F_{\lambda }\\ & \frac{Dv}{Dt}+u\left(f+\frac{u\tan \varphi }{a}\right)=-\frac{1}{a}\frac{1}{\rho }\frac{\partial p}{\partial \varphi }+F_{\varphi }\\ & \frac{Dw}{Dt}=-\frac{1}{\rho }\frac{\partial p}{\partial z}-g+F_z\\ & \frac{D\theta }{Dt}=Q\\ & \frac{\partial \rho }{\partial t}+\frac{1}{a\cos \varphi }\left[\frac{\partial }{\partial \lambda }(\rho u)+\frac{\partial }{\partial \varphi }(rv\cos \varphi \right]+\frac{\partial }{\partial z}(\rho w)=0\\ & p=\rho RT\end{array}$$

where we have used the divergence in spherical coordinates.

$$\frac{Dw}{Dt}=-\frac{1}{\rho }\frac{\partial p}{\partial z}-g+F_z$$

These equations are still not closed because we will need to express the heating/cooling term $Q$ and the friction terms $F$ as a function of the state variables. This will require a theory of the processes that drive them. Where $R=287.052874Jk{g}^{-1}{K}^{-1}$ is the gas constant for dry air and $c_p=1.005$ is the specific heat at constant pressure, $c_v=0.718$ is the specific heat at constant volume, $\kappa =\frac{R}{c_p}$ and $\gamma =c_p/c_v$ is their ratio.

For theoretical and idealized studies the set of equation projected on the $\beta$-plane is also used

$$\begin{array}{rl}& \frac{Du}{Dt}-fv=-\frac{1}{\rho }\frac{\partial p}{\partial x}+F_x\\ & \frac{Dv}{Dt}+fu=-\frac{1}{\rho }\frac{\partial p}{\partial y}+F_y\\ & \frac{Dw}{Dt}=-\frac{1}{\rho }\frac{\partial p}{\partial z}-g+F_z\\ & \frac{D\theta }{Dt}=Q\\ & \frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathbf{v})=0\\ & p=\rho RT\end{array}$$

and the gradient operator is the cartesian operator

$$\nabla =\frac{\partial }{\partial x}+\frac{\partial }{\partial y}+\frac{\partial }{\partial z}$$

and the advective derivative is then

$$\frac{D}{Dt}=\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}+w\frac{\partial }{\partial z}$$

^block-ref